what data structure does a binary tree degenerate to if not balanced properly

April 09, 2022 Post a Comment

Tree

A tree is a often-used data structure to simulate a hierarchical tree structure.

It is already built into a lot of programming laguages.

What is a Tree?

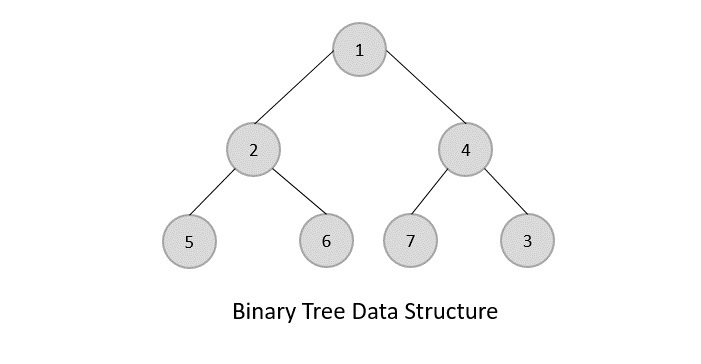
A tree is a collection of nodes.

Root - Node at the top of the tree
Child - Node below a given node continued by its edge downward
Parent - Any node which has 1 edge up to a node. (except root node)
Leafage - Node which does not have whatever child
Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its side by side child node is at level 1, its grandchild is at level ii, then on.
Subtree − Subtree represents the descendants of a node.

Binary Tree

A binary tree is a tree data stucture in which each node has at most two children, which are referred to every bit the left kid and the correct child.

Properties of Binary Tree

There are at well-nigh $2^{i-1}$ nodes on the i-th layer of the binary tree.
Binary Tree with depth yard has at about $ii^k-ane$ nodes.
For any binary tree T, if the number of terminal nodes is $northward$ and the number of nodes with caste 2 is $t$ , then $n=t+1$ .

Each Node at most 2 children

the 2 children are called the left child and the right child

Types of Binary Tree

Let'south choice some to explicate.

Consummate Binary Tree

Basically, a binary tree with all leaves have the same level.

Perfect Binary Tree

Basically, a binary tree with all interior nodes take two children and all leaves have the aforementioned level.

Balanced Binary Tree

Basically, Look like a tree.

Boilerplate instance
Search in O( log(n) ) time
Insert in O( log(n) ) time

Degenerate Binary Tree (Unbalanced)

Basically, Wait like a list. Merely one child.

Worst case
Search in O(due north) time (Linear)
Insert in O(n) time (Linear)

Binary Search Tree

Keypoint: Every round throw abroad half the numbers

Binary Search tree exhibits a special behavior. A node'due south left child must have a value less than its parent's value and the node'due south right child must have a value greater than its parent value.

This ordering property makes finding a node very very fast because nosotros have a pretty proficient idea of where it would be.

In each functioning, we chopped off about half of the nodes.

For case, to find Node value contain 42, I just demand to check is the value larger or smaller than the root? And then I choosed one side of nodes and that already ignored one-half of nodes in the tree and go along the functioning. Now I need to check is the value larger or smaller than the 35? Yeah it is, than I ingored another small half of nodes and constitute the Node value contain 42.

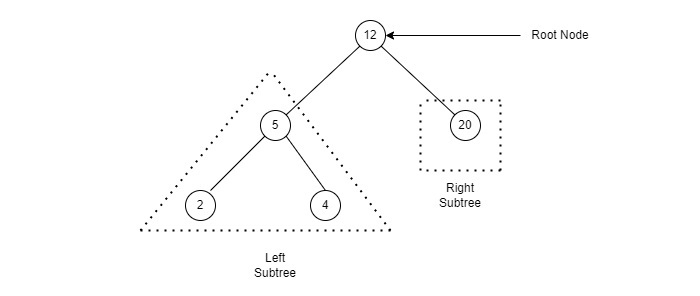
Backdrop of Binary Search Tree

left child value < parent value
right child value > parent value

Code Implementation

                                                      #include                              <iostream>                                                                                
                                                      using                            namespace                            std;                          
                                                    
                                                                                    struct                              node                                                                                
                                                      {                                                    
                                                      int                            data;                          
                                                                              
                                                      node* left;                          
                                                      node* right;                          
                          };                          
                                                    
                                                      node*                              createNode                              (int                                value)                            {                          
                                                      node* newNode =                            new                            node;                          
                                                      newNode->data = value;                          
                                                      newNode->left =                            NULL;                          
                                                      newNode->right =                            NULL;                          
                                                                              
                                                      return                            newNode;                          
                          }                          
                                                    
                                                      node*                              insert                              (node* root,                                int                                data)                                                                                
                                                      {                          
                                                      if                            (root ==                            NULL)                          
                                                      return                            createNode(data);                          
                                                                              
                                                      if                            (data < root->information)                                                    
                                                      root->left =                            insert(root->left, data);                                                    
                                                      else                            if                            (data > root->data)                          
                                                      root->correct =                            insert(root->correct, data);                                                    
                                                                              
                                                      render                            root;                          
                          }                          
                                                    
                                                                                    void                              inorder                              (node* root)                            {                          
                                                      if                            (root ==                            NULL)                          
                                                      render;                          
                                                      inorder(root->left);                          
                                                      cout << root->information << endl;                          
                                                      inorder(root->right);                                                    
                          }                          
                                                    
                                                                                    int                              main                              ()                            {                          
                                                      node *root =                            Aught;                          
                                                      root =                            insert(root,                            8);                          
                                                      insert(root,                            4);                          
                                                      insert(root,                            6);                          
                                                      insert(root,                            three);                          
                                                      insert(root,                            32);                          
                                                      insert(root,                            13);                          
                                                      insert(root,                            16);                          
                                                      insert(root,                            ii);                          
                                                                              
                                                      inorder(root);                          
                          }

Binary Tree Traversal

Binary Tree Traversing, besides known every bit walking through a tree.

Let'due south put a flick to confuse people here:

Inorder Traversal

Basically, Order: left -> root -> correct

Typically in binary search trees nosotros want to do inorder traversals because that actually allows the nodes to exist printed in order.

^ Gild: 1,ii,3

Preorder Traversal

Basically, Order: root -> left -> correct

In this traversal method, the root node is visited first, then the left subbtree and finally the right subtree.

Postorder Traversal

Basically, Lodge: **left -> correct -> root **

In this traversal method, the left node is visited commencement, then the right subbtree and finally the root subtree.

Levelorder Traversal

Basically, Social club: Starting from Level 0 (Left to Correct)

In this traversal method, visit from the start level of the tree (root), then from the tiptop to the lesser levels. If it is in the same level, the nodes are accessed one by one from the left to the right.